SCIENCE

Marshmallows: The Perfect Media for Demonstrating Principles of Physics

The gooey confections turn out to be a must-have for at-home science experiments

March 29, 2013

The gooey confections can be used to measure the speed of light and demonstrate relationships between the volume of a gas and its pressure and temperature. Photo by Flickr user John-Morgan

If the Easter Bunny comes to your house this weekend, you may find yourself with a plethora of marshmallows and Peeps. What to do with them all? Aside from simply eating them, cooking with them, or unleashing your artistic side by making dioramas, consider using them….for science!

Marshmallows, it turns out, are must-have pieces of equipment for at-home science experiments. Sure, you can use them test your kids’ self control through the the field of psychology’s notorious marshmallow test and its ever-more complex iterations. But if you’d rather not torture your kids by leaving tantalizingly in reach a marshmallow they’re ordered not to have, consider trying these easy science projects:

Marshmallows in a vacuum

The relationship between the volume of a gas and its pressure can be demonstrated at home with a simple set up. Photo by Mohi Kumar

No, not that kind of vacuum, despite the intriguing possibilities conjured by this phrase. You’ll need:

A glass jar with a lid
A mechanism to pump some of the air out of the jar
Marshmallows

The Physics Hypertextbook recommends using a kitchen vacuum pump for this experiment. Cutting a small hole in the jar’s lid and squeezing a wine preserver’s vacuum pump into it also works.

Place a few marshmallows in the jar, seal it, and then pump the air out:

What’s going on? Marshmallows are basically a foam spun out of sugar, water, air, and gelatin. The sugar makes them sweet, the water and sugar combo makes them sticky and the gelatin makes them stretchy. But the air–which actually makes up most of the confection’s volume–makes marshmallows the tastiest way to encapsulate a gas in a solid. As you pump air out of the jar, the air inside the marshmallow expands and the marshmallow puffs up. Release the seal, and the marshmallows return to their normal size.

Congratulations! You’ve just demonstrated Boyle’s Law, which states that when the temperature doesn’t change, that the relationship between pressure (which is decreased by pumping air out of the jar) and volume of any set amount of gas (the marshmallow) is inversely proportional. In other words, decreasing one necessitates an increase of the other.

If you can’t eat ‘em, nuke ‘em!

If you’ve ever roasted a marshmallow over a campfire, you’ll know where this next demonstration is going. You’ll need:

A microwave
A microwavable plate
A standard-sized marshmallow (avoid minis or jumbos; the former will fry and the latter may make an enormous mess!)

Place the marshmallow on one of its flat sides in the center of a plate. Then microwave the marshmallow for, say, 45 seconds on high.

It’s alive! This time, rather than changing the pressure surrounding the marshmallow, you’re changing the temperature. As the microwave bakes the marshmallow, the water in the marshmallow heats up and warms the air. When air becomes hot, it expands, forcing the marshmallow to puff up. The confection’s water also softens the sugars, causing it to ooze, as seen in the video above (created by YouTube user bbbpwns).

The relationship between temperature and volume is representative of Charles’ Law, which holds that any set amount of gas will expand when heated–increasing the temperature of a gas necessitates an increase in the gas’ volume.

Trying this with Peeps makes for a slightly alarming outcome, showcased by YouTube user UBrocks:

If you flashed back to the Stay Puft Marshmallow Man, alas–the monster marshmallow you pulled from your microwave doesn’t last–it will cool and deflate into a glob of ooze. But before it cools completely, the ooze is quite malleable and can be sculpted into shapes. But careful! The marshmallow remnants are like naplam–they’ll stick to you and burn. After it cools a bit, brush some oil on your palms before you mold anything, else your sculpture will stay glued to your hands.

A gooey way to calculate the speed of light

For this demonstration you need a bit of background knowledge as you start out. The speed of a wave can be calculated by multiplying the wavelength (the distance from crest to crest) with the frequency (the number of crest-to-crest cycles that repeat in a stretch of time). Light is a wave, and its speed can be calculated the same way without fancy equipment. You’ll need:

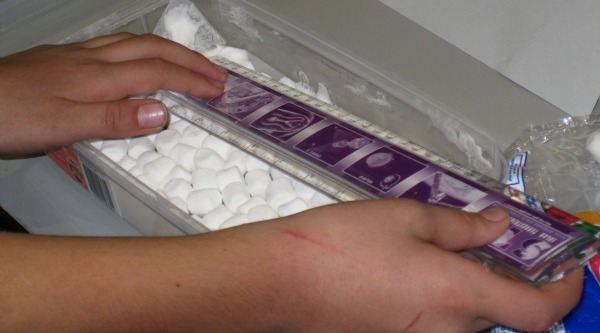
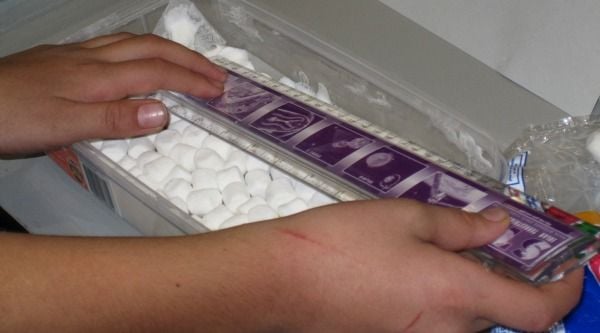
A child measures the distance between melted patches after a layer of marshmallows was microwaved. Photo by Mohi Kumar

A microwave with the turntable removed
A glass casserole dish or baking tray
Mini marshmallows
A ruler
A calculator

Take the baking tray and pack one layer of marshmallows along the bottom, lined up like tiny puffy soldiers. Make sure the turntable is removed from the microwave–this allows microwaves to move through the glass and the marshmallows in a standing wave pattern. Cook for a few minutes on low, watching the marshmallows carefully. With the turntable removed, the microwave doesn’t heat evenly–you’ll notice melted patches forming in your marshmallow field.

As soon as you see a few such patches, remove the dish and measure the distance between two that form a line parallel to the microwave’s door–these mark the locations of highest amplitudes within the standing wave. Multiply this by two to get the full wavelength of the microwaves that passed through your marshmallows (if you look at the geometry of a standing wave, your initial measurement only gave you half the wavelength). Convert this into meters.

Multiplying this result by frequency of the microwave, found in the microwave’s manual or in a label inside the device, gives ~299,000,000 meters per second–roughly speed of light! Catch a video of this here.